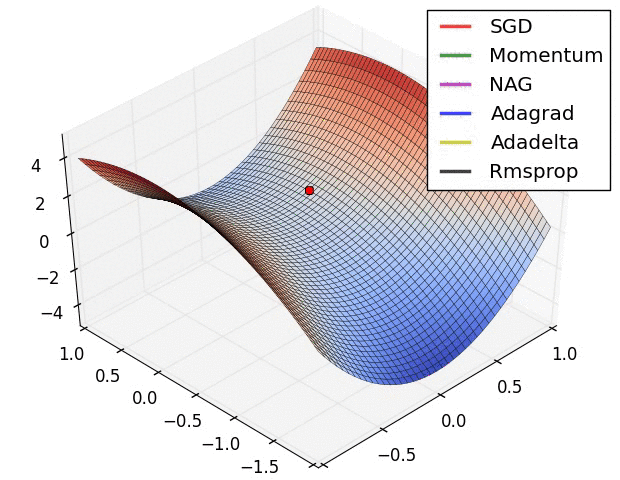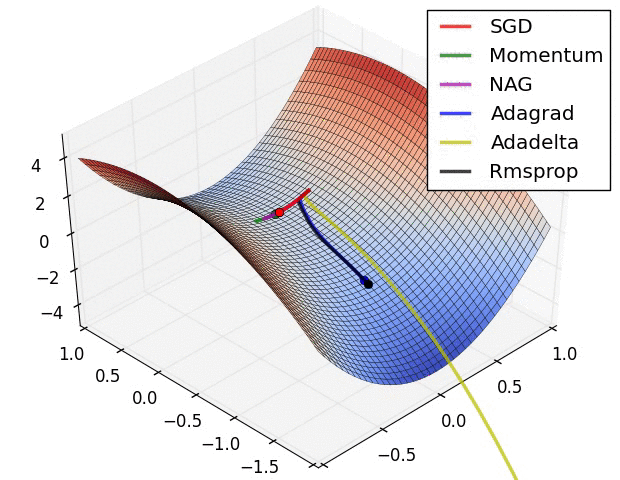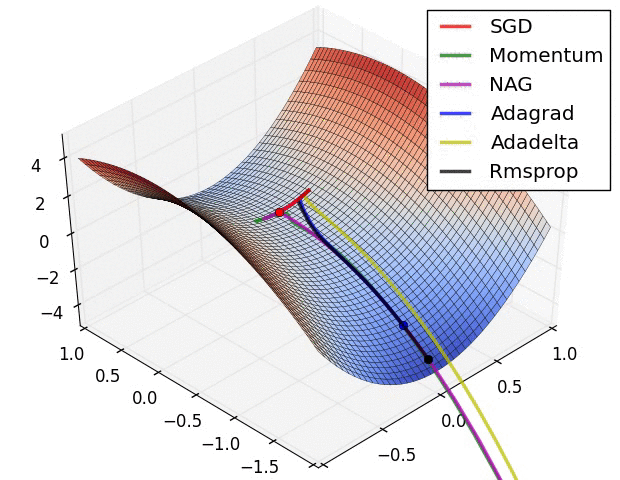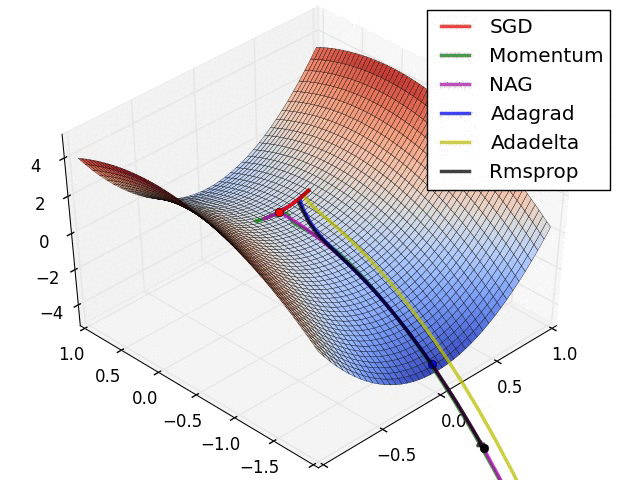
Vanilla gradient descent
Let be the gradient of the error function $E$ w.r.t a weight at update time $t$.
- “Vanilla” gradient descent updates the weight along the nagative gradient direction:where $\eta$ denotes the learning rate.
How to set the learning rate?
Initialize the $\eta$, and update as the training processes
- Learning rate schedules: typically initial larger steps followed by smaller steps for fine tuning: results in faster convergence and better solutions.
Learning Rate Schedules:
- Time-dependent schedules:
- Piecewise constant: pre-determined $\eta$ for each epoch
- Exponential:
, where $r \sim \text{training set size}$ - Reciprocal:
, where $c \sim 1$.
- Performance-dependent $\eta$: fixd $\eta$ until validation set stops improving, then halve $\eta$ each epoch (i.e. constant, then exponential)
Momentum
- Momentum hyperparameter: $\alpha \sim 0.9$
Momentum term encourages the weight change to go in the previous direction
Problems: tuning learning rate and momentum parameters can be expensive.
Adaptive learning rates
- Tuning learning rate parameters is expensive (grid search)
- AdaGrad: normalize the update for each weight
- RMSProp: AdaGrad forces the learning rate to always decrease, this constraint is relexed with RMSProp
- Adam: “RMSProp with momentum”
AdaGrad
- Separate, nomalized update for each weight
- Normalized by the sum squared gradient $S$where $\epsilon \sim 10^{-8}$ is a small constant to prevent division by zero errors.
- The update step for is normalized by the (square root of) the sum squared gradients for that parameter
- Weights with larger gradient magnitudes will have smaller effective learning rates
- cannot get smaller, so the effective learningr rates monotonically decrease
- AdaGrad can decrease the effective learning rate too aggressively in NNs.
RMSProp
- Backgroud: RProp[3] is for batch gradient descent with an adaptive learning rate for each parameter, and uses only the sign of the gradient (equivalent to normalizing by the gradient)
- RMSProp can be viewed as a
stochastic gradient descent version of RProp normalized by a moving average of the squared gradient[4]. It is similar to AdaGrad, but replacing the sum by a moving average for $S$:where $\beta \sim 0.9$ is the decay rate. - Effective learning rates no longer guaranteed to decrease.
AdaDelta
Background:
AdaGrad has two main drawbacks:
- the continual decay of learning rates throughout training;
- the need for a manually selected global learning rate.
Let $\beta$ denote the decay rate.
The numerator of update term is not manually $\eta$, resulting in insensitivity of pre-defined learning rate.
Pros:
- Requires
no manually setting of a learning rate; - insensitive to hyperparameters;
- minimal computation over gradient descent.

where $\text{RMS}[x]_t = \sqrt{E[x^2]_t + \epsilon}$
Adam (ICLR 2015)
- Adam can be viewed as a variant of RMSProp with momentum:where $\alpha \sim 0.9$, $\beta \sim 0.999$, $\epsilon \sim 1e-8$


AdamW (ICLR 2018)

AMSGrad
- AMSGrad[6] maintains the
maximumof all unitl the present time step to normalizing the running average of the gradient instead of directly using in Adam. - AMSGrad results in a non-increasing step size and avoids pitfalls of Adam and RMSProp.
AdaBound
- AdaBound[7] applies a gradient clipping on the learning rate. It behaves like Adam at the beginning as the bounds have little impact on learning rates, and it gradually transforms to SGD.
Rectified Adam (RAdam)
Problems
- Adaptive learning rate has an undesirably large variance due to the lack of samples in the early stage, leading to suspicious local optima.
Previous solution
- Warmup heuistics: using a small learning rate in the first few epochs of training
- E.g. Linear warmup, set , when .
RAdam
Rectified Adam (RAdam) induced a rectification term to mitigate the variance of adaptive learning rate, inspired by Exponential Moving Average (EMA)[10].
Let denote the length of Simple Moving Average (SMA), be the maximum length of the approximated SMA.
if $\rho_t > 4$ i.e., the variance is tractable:
else:

- The heuristic linear warmup can be viewed as setting
Lookahead
Lookahead [11] is orthogonal to 1) adaptive learning rate schemes, such as AdaGrad and Adam, and 2) accelerated schemes, e.g. heavy-ball and Nesterov momentum. It iteratively updates two sets of weights.
Intuition: choose a search direction by loking ahead at the sequence of “fast weights”, generated by another optimizer.
Process: Lookahead first updates the “fast weights” $k$ times using any standard optimizer in the inner loop, before updating the “slow weights” once, in the direction of the final fast weights.
It is empirically robust to the suboptimal hyperparameters, changes in the inner loop optimizer, # of fast weight updates and the slow weights learning rate.
Lookahead optimizer
Lookahead maintains a set of slow weights $\phi$ and fast weights $\theta$,which synced with fast weights every $k$ updates.
- Init parameters , loss function $L$
- sync period $k$, slow weights step size $\alpha$, optimizer $A$
- for t = 1,2,…:
- sync updated slow weights to the inner loop fast weights:
- for i in 1,2,…,k:
- sample mini-batch of data $d \sim \mathcal{D}$
- update fast weights with standard optimizer
- update slow weights with interpolation
After $k$ inner updates using $A$, the slow weights are updated towards the fast weights by linearly interpolating in weight space $\theta - \phi$. Then after each slow weights update, the fast weights are reset to the current slow weights.

- Benefit: Loopahead benefits from large learning rate in the inner loop. The fast weights updates make rapid progress along the low curvature direction, whilst the slow weights help smooth out the oscillation through the parameter interpolation.
Slow weights trajectory
an exponential moving average (EMA) of the final fast weights within each inner loop after $k$ innerloop steps:
Intuition: slow weights use recent fast weights but matain the effect from previous fast weights.
Fast weights trajectory
- maintaining
- interpolating update:
- resetting to current slow weights
Ranger
Ranger[12] applies RAdam as the optimizer $A$ in Lookahead algorithms (source code: [13]).
References
- 1.cs231n neural-networks-3 ↩
- 2.Duchi, J., Hazan, E., & Singer, Y. (2011). Adaptive subgradient methods for online learning and stochastic optimization. Journal of Machine Learning Research, 12(Jul), 2121-2159. ↩
- 3.Riedmiller, M., & Braun, H. (1993, March). A direct adaptive method for faster backpropagation learning: The RPROP algorithm. In Proceedings of the IEEE international conference on neural networks (Vol. 1993, pp. 586-591). ↩
- 4.csc321 Neural Networks for Machine Learning Lecure6 ↩
- 5.Kingma, D. P., & Ba, J. (2014). Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980. ↩
- 6.Reddi, S. J., Kale, S., & Kumar, S. (2019). On the convergence of adam and beyond. arXiv preprint arXiv:1904.09237. ↩
- 7.Luo, L., Xiong, Y., Liu, Y., & Sun, X. (2019). Adaptive gradient methods with dynamic bound of learning rate. arXiv preprint arXiv:1902.09843. ↩
- 8.Loshchilov, I., & Hutter, F. (2017). Fixing weight decay regularization in adam. arXiv preprint arXiv:1711.05101. ↩
- 9.Zeiler, M. D. (2012). ADADELTA: an adaptive learning rate method. arXiv preprint arXiv:1212.5701. ↩
- 10.Liu, L., Jiang, H., He, P., Chen, W., Liu, X., Gao, J., & Han, J. (2019). On the Variance of the Adaptive Learning Rate and Beyond. ArXiv, abs/1908.03265. ↩
- 11.Zhang, M.R., Lucas, J., Hinton, G.E., & Ba, J. (2019). Lookahead Optimizer: k steps forward, 1 step back. ArXiv, abs/1907.08610. ↩
- 12.https://medium.com/@lessw/new-deep-learning-optimizer-ranger-synergistic-combination-of-radam-lookahead-for-the-best-of-2dc83f79a48d ↩
- 13.https://github.com/lessw2020/Ranger-Deep-Learning-Optimizer ↩
