An Introduction to Graph Neural Networks

Graph Neural Networks (GNNs) has demonstrated efficacy on non-Euclidean data, such as social media, bioinformatics, etc.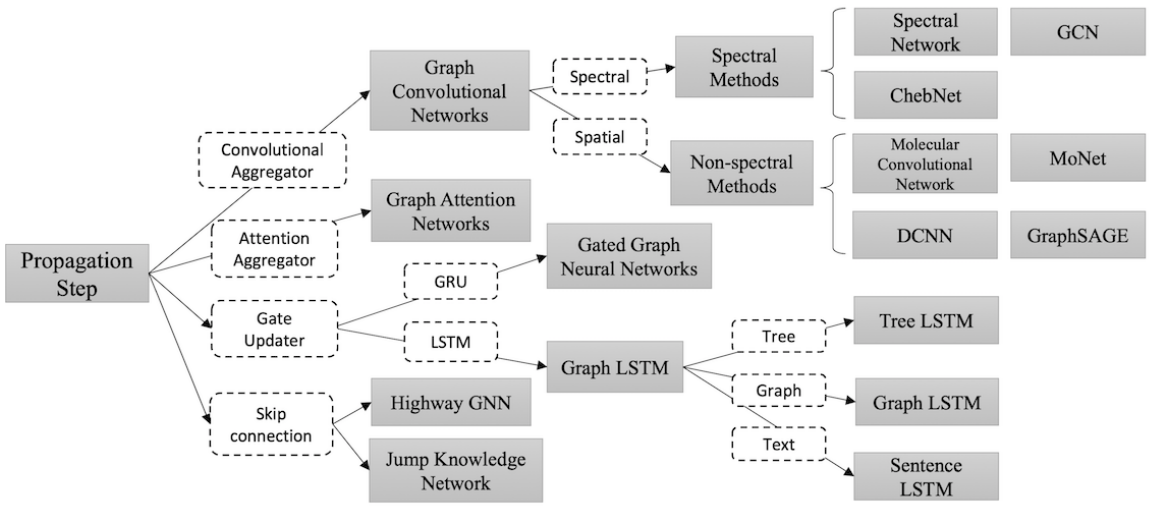

Image source: ^[1]

Related background

Convolution

Denoting $g$ as the filter on $f$, the convolution:

$$(f \star g)(t) = \int_\mathbb{R} f(x) g(t-x) dx$$

Fourier transformation

• Fourier transformation: $$\mathcal{F}\{f\}(v) = \int_\mathbb{R} f(x)e^{-2 \pi i x \cdot v} dx$$

• Inverse Fourier transformation:

  $$\mathcal{F}^{-1}\{f\}(x) = \int_\mathbb{R} f(v)e^{-2 \pi i x \cdot v} dv$$

• The convolution can be rewritten as:

  $$f \star g = \mathcal{F}^{-1}\{\mathcal{F}\{f\} \cdot \mathcal{F}\{g\} \}$$

Spectral methods

Graph Convolutional Networks (GCN)

GCN^[2] applies convolutions in the Fourier domain by computing the eigendecomposition of the graph Lapacian ^[3] using the first-order approximation. When applying convolution on the signal $x$ with the filter $g_\theta = \text{diag}(\theta)$ parameterized by $\theta \in \mathbb{R}^N$ in the Fourier domain, i.e.,

$$\begin{align} f \star g &= \mathcal{F}^{-1}\{\mathcal{F}\{f\} \cdot \mathcal{F}\{g\} \} & \\ g \star x &= U ( \underbrace{ U^\top g}_{g_\theta(\Lambda)} \cdot U^\top x ) & \\ & = U g_{\theta^\prime}(\Lambda) U^\top x & \\ & \approx \theta (I_N + D^{-1/2} A D^{-1/2}) x & \text{Chebyshev polynomials (K-order 1)} \end{align}$$

where $U$ is the matrix of eigenvectors of the normalized graph Laplacian $L = I_N - D^{-1/2} A D^{-1/2} = U \Lambda U^\top$

Let $\tilde{A} = A + I_N, \tilde{D}_{ii} = \sum_{j} \tilde{A}_{ii}$, we get:

$$H^{l+1} = \sigma( \tilde{D}^{-1/2} \tilde{A} \tilde{D}^{-1/2} H^{(l)} W^{(l)})$$

Source code (TensorFlow)
Source code (PyTorch)

• spectral convolution can only be applied on undirected graphs, assuring that $L$ is a symmetric matrix.

Non-spectral methods

GraphSAGE

GraphSAGE is one of the archetype of non-spatial approaches. It samples from the neighborhood in the graph and aggregates the feature information from its local neighborhood.^[4]

Graph Attention Networks (GAT)

Notation:

• Input (node features): $\mathbf{h}= \{ \overrightarrow{h}_1, \overrightarrow{h}_2, \cdots, \overrightarrow{h}_N\}, \overrightarrow{h}_i \in \mathbb{R}^F$, where $N$ is the # of nodes, $F$ is the # of features in each node.
• Output: $\mathbf{h}^\prime= \{ \overrightarrow{h}_1, \overrightarrow{h}_2, \cdots, \overrightarrow{h}_N\}, \overrightarrow{h}_i \in \mathbb{R}^{F^\prime}$, where $F^\prime$ is the output dimension.

1. Pass inputs $\mathbf{h}$ into a learnable shared linear transformation, parameterized by a weight matrix $\mathbf{W} \in \mathbb{R}^{F^\prime \times F}$.
   
2. Perform self-attention on the nodes
   • compute the attention coefficients using a shared attention mechanism $a: \mathbf{R}^{F^\prime \times F} \rightarrow \mathbf{R}$: $$e_{ij} = a (\mathbf{W}\overrightarrow{h}_i, \mathbf{W}\overrightarrow{h}_j) = \text{LeakyReLU} \big( \overrightarrow{\mathbf{a}}^\top [\mathbf{W}\overrightarrow{h}_i \Vert \mathbf{W}\overrightarrow{h}_j] \big)$$
   • Compute $e_{ij}$ for nodes $j \in \mathcal{N}_i$,where $\mathcal{N}_i$ is the neighborhood of node $i$ (including $i$) in the graph. Let $\Vert$ denote concatenation, $$\alpha_{ij} = \text{softmax}_j (e_{ij}) = \frac{e_{ij}}{\sum_{k \in \mathcal{N}_i} \exp (e_{ik}) }$$
3. Multi-head attention. The final output dimension is $\mathbf{R}^{KF^\prime}$, where $k$ is the attention number. $$\overrightarrow{h}^{\prime}_i = \Vert_{k=1}^K \sigma \bigg( \sum_{j \in \mathcal{N}_i} \alpha_{ij}^k \mathbf{W}^k \overrightarrow{h}_j \bigg)$$
4. For the final layer, GAT aggregates neighbor nodes by averaging different node representations: $$\overrightarrow{h}^{\prime}_i = \sigma \bigg( \frac{1}{K} \sum_{k=1}^K \sum_{j \in \mathcal{N}_i} \alpha_{ij}^k \mathbf{W}^k \overrightarrow{h}_j \bigg)$$

Source code (TensorFlow)

Graph Transformer Networks (GTN)

References

---

1. 1.Zhou, J., Cui, G., Zhang, Z., Yang, C., Liu, Z., & Sun, M. (2018). Graph Neural Networks: A Review of Methods and Applications. ArXiv, abs/1812.08434. ↩
2. 2.Kipf, T., & Welling, M. (2016). Semi-Supervised Classification with Graph Convolutional Networks. ArXiv, abs/1609.02907. ↩
3. 3.Laplacian matrix wiki ↩
4. 4.Hamilton, W.L., Ying, Z., & Leskovec, J. (2017). Inductive Representation Learning on Large Graphs. NIPS. ↩
5. 5.Velickovic, P., Cucurull, G., Casanova, A., Romero, A., Liò, P., & Bengio, Y. (2018). Graph Attention Networks. ICLR ↩
6. 6.Yun, S., Jeong, M., Kim, R., Kang, J., & Kim, H.J. (2019). Graph Transformer Networks. NeurIPS. ↩