Softmax encounters large computing cost when the output vocabulary size is very large. Some feasible approaches will be explained under the circumstance of skip-gram pretraining task.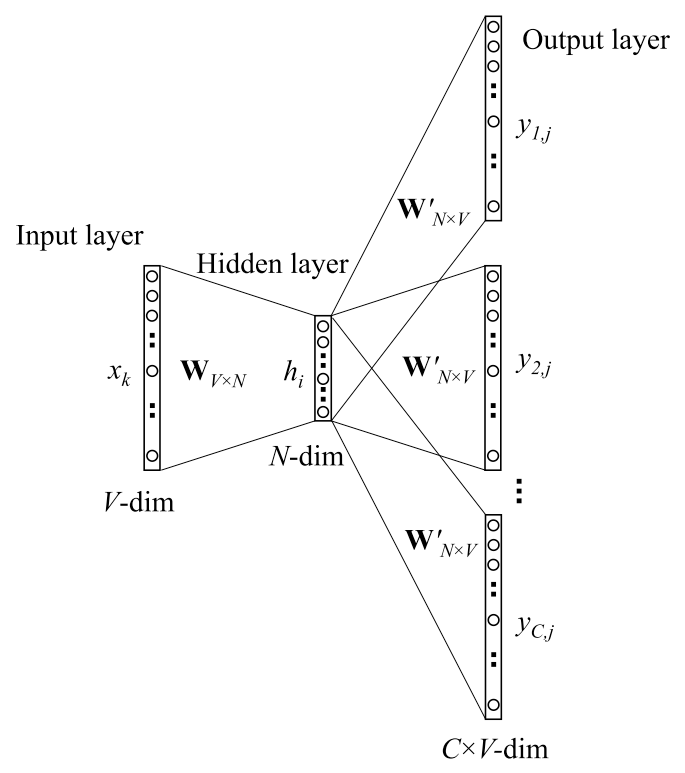
Softmax
The training objective of Skip-gram model is predicting the surrounding words in the sequences. Given a sequence of words w1,w2, …, wT. The final objective is to minimize the average log probability:
The output of skip-gram formula is:
where $v_w$ and $v’_w$ are the “input” vector representation (i.e., the hidden layer output hi in previous fig) and the “output” vectors (i.e., the weights of W’N x V).
Solution
Hierarchical Softmax
Hierarchical Softmax (HSM)[1] reduce the computing cost from $O(V)$ to $O(\log V)$, where V denotes the output vocab size. The V leaf nodes in the binary tree represent the vocabulay words wilst the (V-1) inner nodes denote the probability mass.

For each leaf node, there exits a unique path from the root node to that unit, on which path the probability is estimated along the nodes in the path. As the figure below shown, the highlighted path is from root to the leaf node w2, denoted $n(w,4)$, where $n(w,j)$ denotes the jth node on the path from root to the word $w$.
where $ch(n)$ is the left child of node $n$, $v’_{n(w,j)}$ denote the vector representation of the inner node $n(w,j)$, $\mathbf{h}$ is the output of hidden layer:
$\mathbb{I} \big[ \cdot \big]$ is defined as:
The marked path can be computed as:
It is obvious that
Negative Sampling
Negative Sampling(NEG)[2] selects a subset of negative targets as well as the target to approximate the softmax normalization.
The objective is defined as:
where wO is the output word, is the output vector. $h$ is the hidden layer output, and the values on Skip-gram and CBOW are as descibed in the previous section.
Adaptive Softmax
Adaptive Softmax partition the vocab into clusters, Vh and Vt, representing the head of distribution consisting of the most frequent words and the tail denoting rare words. Each cluster is regarded as independent, and the capacity of clusters are adaptive. [2] found that the small number of clusters can obtain comparable results as the original softmax on the very large vocabulary size.
References
- 1.Rong, X. (2014). word2vec Parameter Learning Explained. ArXiv, abs/1411.2738. ↩
- 2.Mikolov, T., Sutskever, I., Chen, K., Corrado, G.S., & Dean, J. (2013). Distributed Representations of Words and Phrases and their Compositionality. NIPS. ↩
- 3.Mohammed, A.A., & Umaashankar, V. (2018). Effectiveness of Hierarchical Softmax in Large Scale Classification Tasks. 2018 International Conference on Advances in Computing, Communications and Informatics (ICACCI), 1090-1094. ↩
- 4.Grave, E., Joulin, A., Cissé, M., Grangier, D., & Jégou, H. (2016). Efficient softmax approximation for GPUs. ArXiv, abs/1609.04309. ↩
- 5.Baevski, A., & Auli, M. (2018). Adaptive input representations for neural language modeling. arXiv preprint arXiv:1809.10853. ↩
