Notes of lectures by D. Silver.
Monte-Carlo Learning
- MC methods learn directly from episodes of experience
- MC is model-free: no knowledge of MDP transitions / rewards.
- MC learns from complete episodes: no bootstrapping
- MC uses the simplest possible idea: value = mean return
- Caveat: can only apply MC to episodic MDPs
- All episodes must terminate
MC policy evaluation
- Goal: learn from episodes of experience under policy $\pi$
- The return is the total discounted reward:
- The value function is the expected return:
- Monte-Carlo policy evaluation uses empirical mean return instead of expected return
First-visit MC policy evaluation
To evaluate state $s$
- The first time-step $t$ that state $s$ is visited in an episode
- Increment counter $N(s) \leftarrow N(s) + 1$
- Increment counter
- Value is estimated by mean return $V(s) = S(s) / N(s)$
- By law of large numbers, $V(s) \rightarrow v_{\pi}(s)$ as $N(s) \rightarrow \infty$
Every-visit MC policy evaluation
To evaluate state $s$
- The every time-step $t$ that state $s$ is visited in an episode
- Increment counter $N(s) \leftarrow N(s) + 1$
- Increment counter
- Value is estimated by mean return $V(s) = S(s) / N(s)$
- By law of large numbers, $V(s) \rightarrow v_{\pi}(s)$ as $N(s) \rightarrow \infty$
Incremental Monte-Carlo
Incremental Mean
The mean of a sequence can be computed incrementally
Incremental MC updates
- Update $V(s)$ incrementally after episode $S_1, A_1, R_2, \cdots, S_T$
- For each state with return
- In non-stationary problems, it can be useful to track a running mean, i.e. forget old episodes
Temporal-Difference Learning
- TD methods learn directly from episodes of experience
- TD is model-free: no knowledge of MDP transitions / rewards
- TD learns from incomplete episodes, by bootstrapping
- TD updates a guess towards a guess
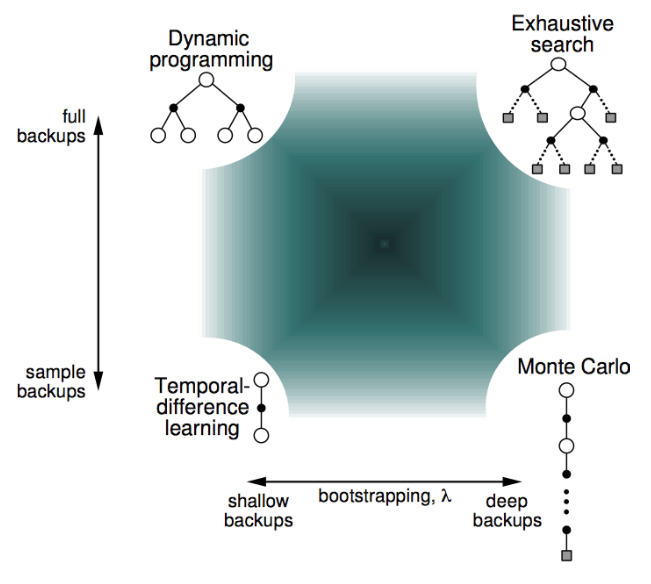
MC and TD
- goal: learn online from experience under policy $\pi$
Incremental every-visit MC
Update value toward actual return
- Simplest temporal-difference learning algorithm: TD(0)
- Update toward estimated return
MC v.s TD
Pros and cons
1.Process
TD can learn before knowing the final outcome
- TD can learn online after every step
- MC must wait until end of episode before return is known
TD can learn without the final outcome
- TD can learn from incomplete sequences
- MC can only learn from complete sequences
- TD works in continuing (non-terminating) environments
- MC only works for episodic (terminating) environments
2.Statistics
- MC has high variance, zero bias
- Good convergence properties (even with function approximation)
- Not very sensitive to initial value
- Very simple to understand and use
- TD has low variance, some bias
- Usually more efficient than MC
- TD(0) converges to but not always with function approximation
- More sensitive to initial value
3.Markov property
- TD exploits Markov property
- Usually more efficient in Markov environments
- MC does not exploit Markov property
- Usually more efficient in non-Markov environments
Bias / Variance trade-off
- Return is unbiased estimate of
- True TD target is unbiased estimate of
- TD target is biased estimate of
- TD target is much lower variance that the return:
- Return depends on many random actions, transitions, rewards
- TD target depends on one random action, transition, reward
